A2 - Thermodynamics
We start this topic by looking at the wonderful Born Haber cycles. This builds on form our work on Hess's law, we construct a more complicated cycle but in the shape of a tall building. If we know the height (energy change) on one side, the other side has the same height. If one piece is missing, we can work it out on this basis. Exothermic processes move up, endothermic processes move down. Look carefully at the example below. Be really careful of the values that you use, for example, if it is MgCl2. then you will need to atomise chlorine and get 2 moles of Cl, then you need 2 lots of the first electron affinity of chlorine.
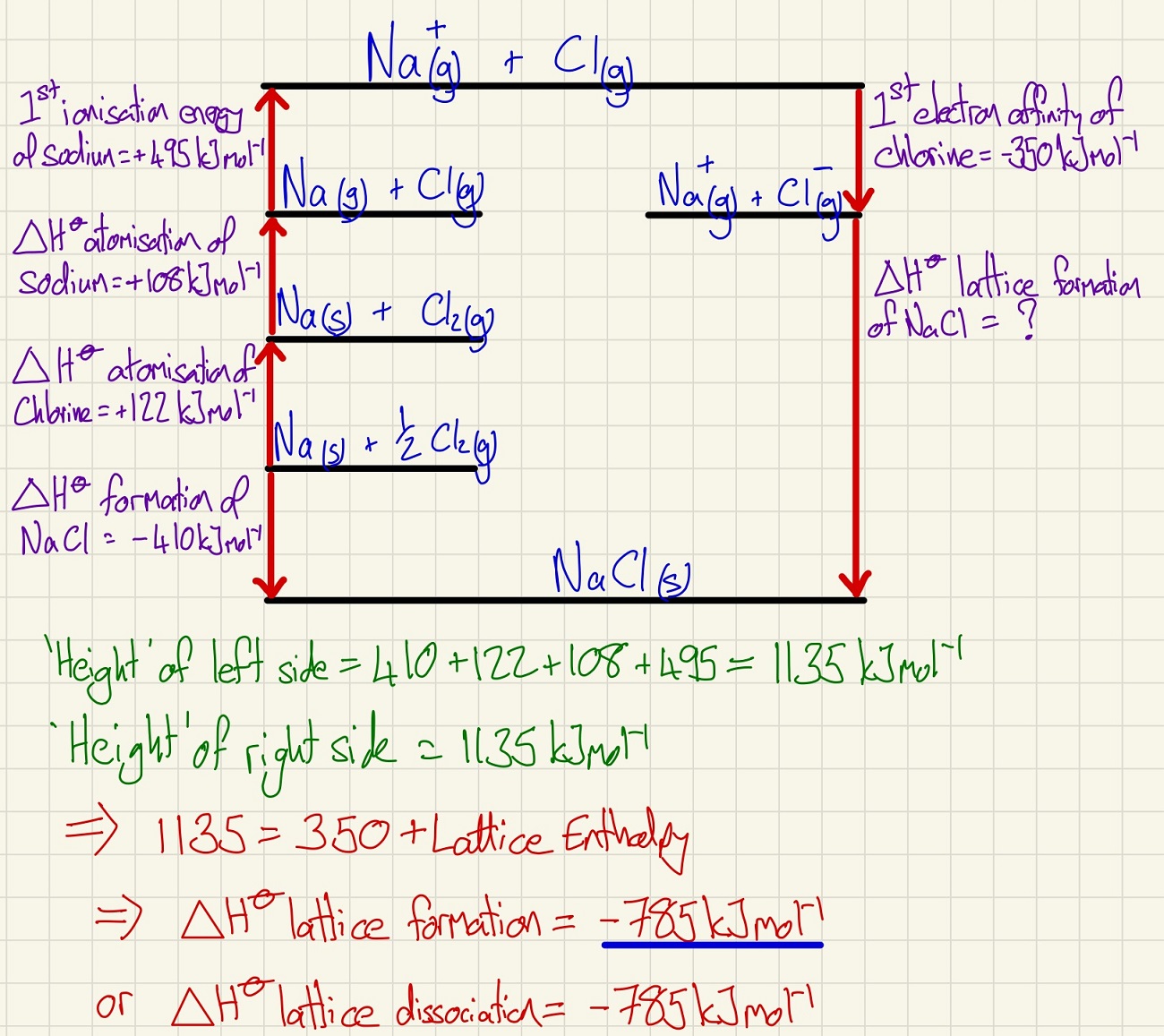
We cannot measure the lattice enthalpy experimentally, this is why we need the Born Haber cycle. However, you may be given this value and asked to work out another process instead. There are two values for lattice enthalpy, dissociation = endothermic and formation = exothermic.

The size of the lattice enthalpy is proportional to the strength of the ionic bonds so Al2O3 has a much higher value because aluminium is 3+ and oxygen is 2-. Aluminium is also a very small ion that is highly charged giving it a high charge density.

The theoretical lattice enthalpy can also be calculated using a very complicated formula. When compared to the actual lattice enthalpy, there will be a difference. This is because no ionic substance is truly 100% ionic, this is because ions can be slightly distorted in the lattice due to attractions. The smaller the difference, the more ionic it is and the bigger the difference, the more covalent character it has.

Entropy is simply a measure of disorder. Highly disordered substances (gases) have high entropy and ordered substances (metals) have low entropy. Find the total entropy of the products and take the total entropy of the reactants.

Gibbs free energy amalgamates entropy and enthalpy to see if a reaction is feasible. If the outcome of the equation is positive, the reaction is not feasible and if it is negative, it should be spontaneous at that temperature.

By rearranging the formula, you can use the data for entropy and enthalpy to see at what temperature a reaction will become spontaneous.

This page was updated on: 3rd November 2023


